1103. Подсчет путей

По заданному ориентированному графу g необходимо определить количество разных циклов, имеющих длину меньше k. Поскольку это количество может быть большим, вычислить его следует по модулю m. Циклом называется непустая последовательность вершин (необязательно различных), в которой из каждой предыдущей вершины в следующую ведет ребро, а также существует ребро, ведущее из последней вершины в первую. Два цикла считаются различными, если последовательности вершин, их определяющие, разные.

Вход. Первая строка содержит количество вершин в графе n (1 ≤ n ≤ 35) и числа k (1 ≤ k ≤ 10⁶) и m (1 ≤ m ≤ 10⁹). Следующие n строк описывают граф: j -ый символ i - ой строки матрицы смежности указывает на присутствие ребра, ведущего из вершины i в вершину j ('Y' означает, что ребро есть, 'N' означает, что нет).

Выход. Вывести одно число – количество разных циклов в g, длины которых меньше чем k. Вывести результат по модулю m.

Пример входа	Пример выхода
4 6 100 NYNY NNYN YNNN YNNN	12

РЕШЕНИЕ

графы

Анализ алгоритма

Теорема. Пусть А – матрица смежности графа. Тогда A^k[i][j] содержит количество путей, ведущих из i -ой вершины в j -ую, и имеющих длину k. Число циклов, имеющих длину k, равно сумме диагональных элементов матрицы A^k.

Определение. Следом матрицы называется сумма ее диагональных элементов.

Количество разных циклов длины, меньшей k, равно сумме диагональных элементов матрицы S = A + A² + A³ + … + A^k-1. Возведение в степень A^k можно совершить за O(n³log k), где n – размер матрицы А (умножение двух матриц размера n совершается за O(n³)). Рассмотрим алгоритм вычисления матрицы S за время O(n³log² k). В нем следует O(log k) раз возводить матрицу A в степень k.

Пусть функция sum(k) вычисляет значение суммы A + A² + … + A^k, а pow(k) находит A^k.

Если k четное, то

sum(k) = A + A² + … + A^k = A + A² + … + A^k/2 + A^k/2+1 + … + A^k =

= (A + A² + … + A^k/2) + A^k/2 * (A + A² + … + A^k/2) =

= sum(k / 2) * pow(k / 2) + sum(k / 2)

Если k нечетное, то

sum(k) = A + A² + … + A^k =

(A + A² + … + A^{k – 1}) * A + A = sum(k – 1) * A + A

Ответом на поставленную задачу будет значение следа матрицы sum(k – 1).

Указанную сумму можно вычислить и по-другому. Построим матрицу B размера 2n * 2n:

B =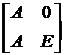

Тогда

B^k =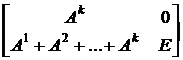

Реализация алгоритма

Переопределим типы линейного массива vi и матрицы (двумерного целочисленного массива) vvi. Матрицу смежности сохраняем в массив строк g.

typedef vector<int> vi;

typedef vector<vector<int> > vvi;

vector<string> g;

char line[50];

Сложение матриц a и b по модулю mod.

vvi add(vvi &a, vvi &b, int mod)

{

int i, j, n = a.size();

vvi c(n, vi(n));

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

c[i][j] = (a[i][j] + b[i][j]) % mod;

return c;

}

Умножение матриц a и b по модулю mod.

vvi mult(vvi &a, vvi &b, int mod)

{

int i, j, k, s, n = a.size();

vvi c(n, vi(n));

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

{

for(s = k = 0; k < n; k++)

s = (s + (long long)a[i][k] * b[k][j]) % mod;

c[i][j] = s;

}

return c;

}

Вычисление матрицы a^k по модулю mod.

vvi pow(vvi &a, int k, int mod)

{

int i, n = a.size();

vvi res(n, vi(n, 0));

for(i = 0; i < n; i++) res[i][i] = 1;

while (k > 0)

{

if (k % 2) res = mult(res, a, mod);

a = mult(a, a, mod);

k /= 2;

}

return res;

}

Вычисление суммы sum(k) = a + a² + a³ + … + a^k.

vvi sum(vvi a, int k, int mod)

{

if (k == 1) return a;

if (k % 2)

{

vvi temp = sum(a,k-1,mod);

return add(mult(temp,a,mod),a,mod);

}

vvi temp = sum(a,k/2,mod);

vvi powk_2 = pow(a,k/2,mod);

return add(mult(temp,powk_2,mod),temp,mod);

}

Функция countTours возвращает количество разных циклов в графе g, длины которых меньше чем k, взятое по модулю m.

int countTours(vector<string> &g, int k, int m)

{

int i, j, n = g.size();

vvi mas(n, vi(n, 0));

long long res;

Преобразуем матрицу смежности из массива строк g в двумерный целочисленный массив mas.

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

if (g[i][j] == 'Y') mas[i][j] = 1; else mas[i][j] = 0;

res = 0;

В матрице temp вычислим сумму a + a² + a³ + … + a^k-1. Все вычисления проводим по модулю m.

vvi temp = sum(mas,k-1,m);

В переменной res находим след матрицы temp.

for(i = 0; i < n; i++)

res = (res + temp[i][i]) % m;

return res;

}

Основная часть программы.

int main(void)

{

scanf("%d %d %d\n",&n,&k,&m);

g.clear();

for(i = 0; i < n; i++)

{

gets(line);

g.push_back(line);

}

res = countTours(g,k,m);

printf("%d\n",res);

}